Parafrasando Tolstoj[1] «Tutti i sistemi semplici sono semplici allo stesso modo; ogni sistema complesso è complesso a modo suo». Ma cos’è un sistema complesso? Certamente la varietà è uno dei suoi evidenti aspetti ma dietro di esso ci sono alcune caratteristiche comuni.
Non esiste una definizione canonica di complessità, cioè in grado di cogliere tutte le sfumature del termine in modo unanime e condiviso, una definizione che quindi non generi fraintendimenti.
Innanzi tutto sicuramente “complesso” differisce da “semplice” ma occorre precisare che comunque “complesso” non è sinonimo di “complicato”. Un aereo è certamente complicato, con centinaia di migliaia di componenti e funzioni, ma non per questo è complicato: il suo funzionamento interno e il suo moto possono essere descritti sulla base di poche grandezze ed alcune semplici leggi.
Con un altro esempio il sistema nervoso degli insetti si ripete identico in tutti gli esemplari di una data specie, selezionato durante l’evoluzione di queste per svolgere certe funzioni e con limitata capacità di apprendimento: è certamente complicato ma la sua rigidità non lo rende particolarmente complesso. Di contro, il sistema nervoso umano è probabilmente quanto di più complesso si possa avere, per qualcuno persino nell’intero Universo: le sue connessioni sono in parte casuali, non sono ottimizzate in partenza per svolgere i compiti e soprattutto cambia e si adatta imparando dall’esperienza. Rita Levi Montalcini definiva il cervello un accrocco evolutosi riciclando di volta in volta quel che c’era a disposizione e adattandone le parti a nuove funzioni. Un accrocco estremamente complesso.
In poche parole, si può anticipare una definizione di sistema complesso inteso come qualcosa di cui si può parlare a lungo, ovvero più cose possiamo dire sul comportamento di un sistema, più ricco è il linguaggio da usare, più variegata la sua descrizione, maggiore è la complessità del sistema. E se state pensando ai trattati filosofici non posso darvi torto in quanto a complessità.
Tornando ad essere seri facciamo due esempi e compariamoli. Un bicchiere d’acqua e un cane. Per quanto riguarda l’acqua una volta che se ne conoscano temperatura e pressione in genere non c’è altro da dire (a meno che non ci si trovi in quelle condizioni in cui due fasi, ad esempio liquido e solido, coesistono), ed è del tutto inutile cercare di specificare tutte le posizioni e le traiettorie di ogni singola molecola d’acqua perché esiste un unico stato macroscopico: quello determinato dalla temperatura e dalla pressione. Un bicchiere d’acqua è un sistema semplice.
Un cane, invece, ha una ricca descrizione di stati, e ognuno può essere scomposto in altri: può saltare, abbaiare, stare seduto, correre, scodinzolare, e da uno qualsiasi di questi comportamenti può passare rapidamente ad un altro. E ciò lo rende un sistema complesso.
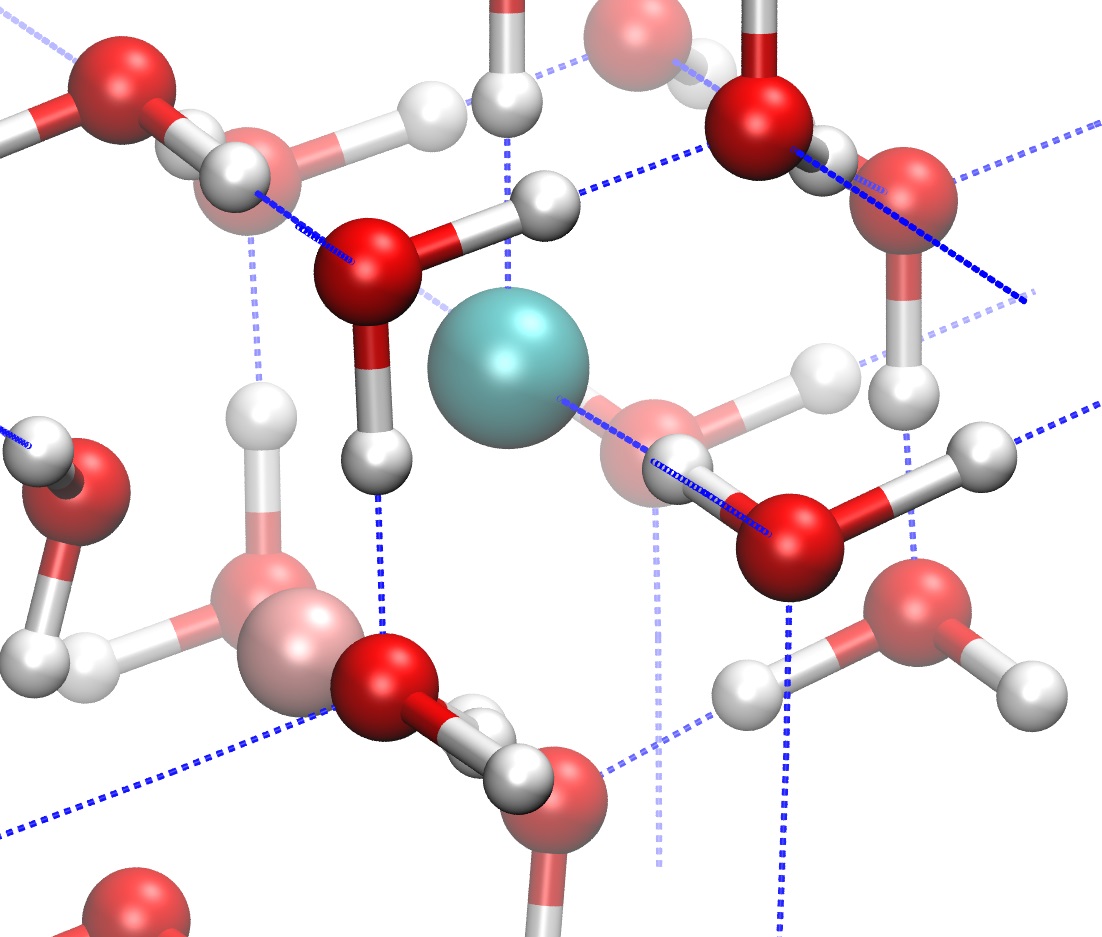Ancora, confrontiamo un cristallo con un vetro: ogni cristallo ha una struttura cristallina che si ripete nello spazio, identica a se stessa e può essere identificato con pochi parametri; un vetro è un sistema disordinato con gli atomi e le molecole che possono trovarsi in un innumerevole di configurazioni diverse.
E possiamo dire lo stesso dei polimeri biologici come quelli che costituiscono le proteine o gli acidi nucleici DNA ed RNA, che possono esistere in moltissimi stati diversi di ripiegamento e passare dall’uno all’altro rapidamente.
Quindi, riformulando, un sistema complesso è caratterizzato dal fatto di poter esistere in tanti stati macroscopici, tutti rilevanti, e di poter passare velocemente da uno stato a un altro[2]. E ciò rende impossibile prevedere in modo esatto il comportamento macroscopico di questi sistemi. Sottolineo macroscopico perché sappiamo dalla Meccanica Quantistica che avvicinandosi alle dimensioni del mondo atomico e subatomico, il microscopico, la determinazione dello stato di un sistema o meglio, di una delle sue grandezze osservabili, abbandona definitivamente il mondo deterministico potendo coesistere ad esempio in due stati contemporaneamente, indeterminati e non prevedibili, che diventano reali solo al momento della misura.
L’idea e i concetti di base da applicare invece ai sistemi macroscopici complessi risalgono ai lavori di Ludwig Boltzmann che inventò la Meccanica Statistica, in grado di calcolare la distribuzione di probabilità delle molte diverse realizzazioni microscopiche (a livello atomico) di un determinato macrostato: in parole più che semplici temperatura e pressione dell’acqua in un bicchiere dipendono dalla media statistica delle energie delle singole molecole (i microstati) che compongono l’acqua (il macrostato) in un determinato momento.
Ma nella meccanica statistica dei sistemi complessi le cose…si complicano! E parecchio perché in questi casi si calcola la probabilità di avere certi macrostati e si determinano le relazioni tra di essi, oppure si calcola il tempo medio che un sistema passa in un certo macrostato piuttosto che in altri possibili. Si tiene in altre parole conto delle relazioni e nelle interazioni tra i possibili innumerevoli macrostati.
Una delle conseguenze della complessità è che un sistema complesso è tale che piccoli cambiamenti nella sua dinamica lo fanno passare in uno stato completamente diverso: è il caos, un comportamento “caotico” in senso stretto perché i sistemi caotici dipendono fortemente dalle condizioni iniziali, basta una loro variazione insignificante che le traiettorie, dopo un certo tempo, saranno completamente differenti. Ed è proprio questo il modo di comportarsi dei sistemi complessi: piccolissime perturbazioni hanno effetti enormi sui macrostati.
E arriviamo ad un punto complicato ma non troppo. Le condizioni iniziali, l’input di un sistema complesso, possono essere addirittura amplificate, rendendo l’evoluzione conseguente ancor più caotica e imprevedibile. Si tratta della cosiddetta Risonanza Stocastica che è parte integrante dei sistemi complessi, altresì detti sistemi dinamici non lineari, che non evolvono nel tempo con linearità e prevedibilità, e della teoria del caos. In alcuni sistemi non lineari si può osservare una certa frequenza caratteristica, si mostrano in cicli evidenti, al momento in cui una determinata quantità di rumore di fondo produce un’amplificazione del segnale (non tutto il rumore di fondo copre il segnale, a volte può esaltarlo).
La prima volta che si teorizzò questo fenomeno fu all’inizio degli anni ’80, per spiegare un apparente paradosso climatico.
Era noto da tempo, dati paleoclimatici alla mano, che nel corso della storia della Terra si sono succedute, più o meno ogni 100.000 anni, variazioni di temperatura dell’ordine di 10 °C, strettamente correlate con il flusso di energia proveniente dal Sole che, a causa dell’ellitticità dell’orbita terrestre, dell’inclinazione dell’asse e delle sue variazioni, e della cosiddetta precessione degli equinozi[3], cambia periodicamente con cicli di periodo simile (sono i cosiddetti, e piuttosto famosi, Cicli di Milanković).
Approfondendo si notò immediatamente che le variazioni dell’energia solare sono insufficienti da sole a spiegare i cambiamenti di temperatura osservati: ed ecco che entra in gioco la risonanza stocastica. La circolazione atmosferica e quella oceanica hanno dinamiche certamente complesse ma possono essere correlate a periodi molto più brevi dei cicli di 100.000 anni: possiamo quindi considerarle come un rumore, combinate con i cambiamenti periodici del flusso di energia solare inducono grandi variazioni della temperatura globale.
Oltre alle ovvie applicazioni in climatologia, nel corso degli anni si è capito che la risonanza stocastica è un fenomeno generale, del quale sono state trovate centinaia di manifestazioni e applicazioni (dall’ottica alla chimica, dalla biologia all’economia finanziaria) e addirittura in un gambero d’acqua dolce che possiede un sistema di recettori in grado di rivelare, mediante il meccanismo della risonanza stocastica, i deboli movimenti d’acqua prodotti dall’avvicinarsi di un predatore.
Nella figura successiva sono illustrati i cicli di variazione relativa della temperatura media della Terra.
Tornando alla climatologia, argomento molto di moda da qualche anno a questa parte, appare evidente che, oltre ad essere una scienza relativamente giovane[4], è strettamente legata alla complessità ed alle leggi probabilistiche dei sistemi non lineari, con parametri tali per cui le condizioni iniziali possono variare a volte inavvertitamente ma provocare enormi cambiamenti nell’evoluzione del sistema. Tant’è che ancora oggi le cosiddette previsioni del tempo si fanno in qualche modo al contrario. Si elabora un modello climatico, lo si confronta con i dati climatici e meteorologici di un evento certo, misurato, e si annota la sua adeguatezza, applicandolo poi a quanto potrebbe accadere in futuro.
Ma, anche se il clima è sempre cambiato, e continuerà a cambiare, anche se la complessità regna sovrana nella fisica teorica alla base delle determinazioni e delle previsioni complessive (non quelle relative al se pioverà domani!), anche se Milanković aveva intuito qualcosa all’inizio del XX secolo[5] non va certo accantonata la realtà dei fatti: che occorre prepararsi ad adattarsi al massiccio e veloce cambiamento climatico in atto dovuto soprattutto alla componente antropica che ha certamente accelerato un fenomeno probabilmente già in atto ma con tempi maggiori. Sempre che non sia troppo tardi per adattarsi, contromisure o meno.
La risonanza stocastica del gambero non ci aiuterebbe affatto.
Nella figura precedente l’architettura d’insieme delle fibre nervose cerebrali dove vengono illustrati gli orientamenti delle stesse: rosso=sinistra-destra, verde=anteriore-posteriore, blu=trasversale al tronco cerebrale.
[1] «Tutte le famiglie felici sono uguali, ogni famiglia infelice è infelice a modo suo». Lev Tolstoj. “Anna Karenina”, 1877.
[2] Come direbbe Giorgio Parisi, Nobel per la fisica nel 2021 proprio per i suoi studi sui sistemi complessi.
[3] Per approfondire si veda la scheda sui Moti della Terra in Wikipedia.
[4] Le prime ricerche serie risalgono alla Seconda Guerra Mondiale, dove i vari reparti di Meteorologia e Climatologia delle Aeronautiche Militari cercavano di fare previsioni il più possibile precise, per ovvi motivi.
[5] Va doverosamente notato, tanto per complicare ancor di più il tutto, che la teoria di Milanković sui cambiamenti climatici non risulta tuttavia ancora perfezionata; in particolare la risposta climatica più grande è relativa a una scala temporale di 400 000 anni, ma gli effetti su questi periodi, per quanto riguarda le glaciazioni, sono apparentemente lievi e non concordano con le previsioni. Per giustificare questa discrepanza, sono chiamati in causa vari fenomeni.
